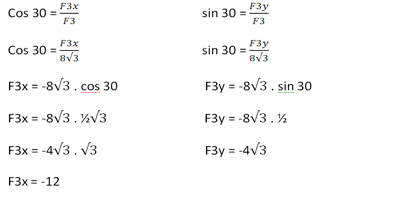Penjumlahan Vektor Secara Analitik | Beserta Contoh Soal

Ittekcno.blogspot.com – apa sich yang dimaksud dengan penjumlahan vektor secara analitik ? pada dasarnya penjumlahan vector dengan metode ini dilakukan dengan cara menjumlahkan komponen-komponen dari sebuah vector itu sendiri.

Sebelumnya kita telah mempelajari tentang bagaimana cara menguraikan vektor dan bagaimana menjumlahkan vector secara grafis. Kedua materi tersebut sangat berkaitan erat dengan apa yang akan kita pelajari kali ini.

Pejumlahan Vektor dengan metode analitik

Seperti yang terlihat pada gambar di atas, kita mempunyai dua buah vektor yaitu vektor a dan vektor b. dan berdasarkan apa yang telah kita pelajari sebelumnya bahwa untuk menjumlahkan vector, terlebih dahulu kita harus memposisikannya ke dalam koordinat kartesius.

Kalau kedua vektor tersebut kita jumlahkan secara grafis, maka akan terlihat seperti ini :

Sedangkan kalau kita ingin menjumlahakannya dengan menggunakan metode analitik, maka akan terlihat seperti ini :

Dari gambar di atas, kita dapat mengetahui semua komponen vektor yang ada. Komponen-komponen inilah yang akan kita jumlahkan, dimana akan membuktikan bahwa hasil jumlah dari komponen vektor a dan vektor b akan sama besar dengan R.

Sehingga dapat kita ketahui :

a = ax + ay, dan

b = bx + by

maka :

Agar lebih jelas lagi, mari kita lihat contoh soal di bawah ini.

Baca juga :

cara mencari komponen vektor

penguraian vektor

Contoh soal 1 :

Gambar di atas menyajikan sebuah diagram vector F1 dan F2. Persamaan yang tepat untuk resultan R = F1 + F2 adalah…

A. 2i + 2j

B. 2i + 4j

C. 4i + 2j

D. 4i + 4j

jawab :

perhatikan option jawaban di atas, karena jawaban yang diminta adalah dalam bentuk vektor satuan, maka kita akan menuliskan besar resultannya dalam bentuk vektor satuan juga.

Dari gambar di atas dapat diketahui :

F1x = 4 F2x = 0

F1y = 2 F2y = 2

Sehingga :

F1 = 4i + 2j

F2 = 0i + 2j

Maka :

R = F1 + F2

= ( 4i + 2j ) + ( 0i + 2j )

= 4i + 4j

Jadi jawaban yang benar adalah option D.

Contoh soal 2 :